Банк заданий ЕГЭ по профильной математике - страница 177
Вопросы
На фабрике керамической посуды 30% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 55% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.
На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 60% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.
Две фабрики выпускают одинаковые стёкла для автомобильных фар. Первая фабрика выпускает 55% этих стёкол, вторая — 45%. Первая фабрика выпускает 4% бракованных стёкол, а вторая — 2%. Найдите вероятность того, что случайно купленное в магазине стекло для автомобильной фары окажется бракованным.
Две фабрики выпускают одинаковые стёкла для автомобильных фар. Первая фабрика выпускает 30 % этих стёкол, вторая — 70 %. Первая фабрика выпускает 5 % бракованных стёкол, а вторая — 4 %. Найдите вероятность того, что случайно купленное в магазине стекло для автомобильной фары окажется бракованным.Вероятность того, что стекло сделано на первой фабрике и оно бракованное: 0,3 · 0,05 = 0,015.
Вероятность того, что стекло сделано на второй фабрике и оно бракованное: 0,7 · 0,04 = 0,028.
Поэтому по формуле полной вероятности вероятность того, что случайно купленное в магазине стекло окажется бракованным равна 0,015 + 0,028 = 0,043.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что разница выпавших очков равна 1 или 2.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 5 или 6.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 2. Результат округлите до сотых.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 7. Результат округлите до сотых.
Найдите объём многогранника, вершинами которого являются точки B, C, D, E, B₁, C₁, D₁, E₁ правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 14, а боковое ребро равно 6.
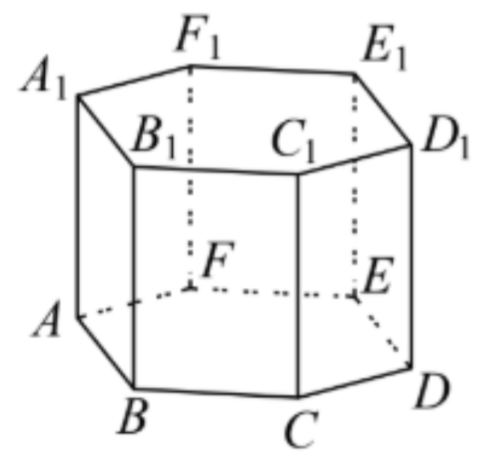
Найдите объём многогранника, вершинами которого являются точки B,C,D,E,B₁,C₁,D₁,E₁ правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 5, а боковое ребро равно 14.