Банк заданий ЕГЭ по профильной математике - страница 179
Вопросы
В треугольнике ABC угол C равен 32°, AD — биссектриса, угол BAD равен 23°. Найдите угол ADB. Ответ дайте в градусах.

Даны векторы 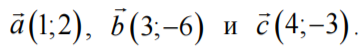 Найдите значение выражения
Найдите значение выражения 
Найдите объём многогранника, вершинами которого являются точки D , A1, B1, D1 прямоугольного параллелепипеда ABCDA1 B1 C1 D1 ,у которого AB = 2 , AD = 9 , AA1 = 5.

Площадь ромба равна 24. Одна из его диагоналей равна 6. Найдите длину другой диагонали.
Длина вектора а равна 15√2, угол между векторами а и b равен 135°, а скалярное произведение а и b равно -120. Найдите длину вектора b.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 16. Найдите угол между прямыми А1D1 и FF1.
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 23 пассажиров, равна 0,95. Вероятность того, что окажется меньше 13 пассажиров, равна 0,52. Найдите вероятность того, что в понедельник число пассажиров автобуса будет от 13 до 22 включительно.
Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 3. Какова вероятность того, что было сделано два броска? Ответ округлите до сотых.
Найдите корень, уравнения 49х-9=1/7.
Найдите значение выражения 
