Банк заданий ЕГЭ по профильной математике - страница 176

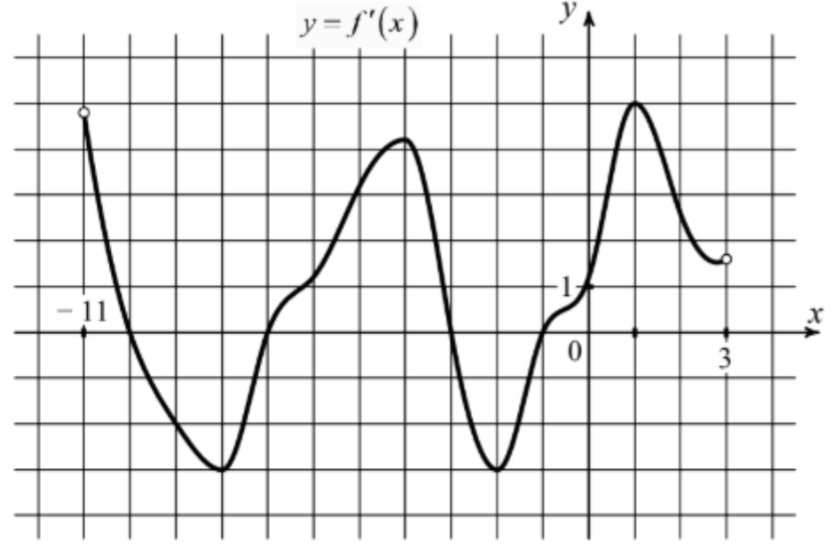
На рисунке изображён график функции y=f'(x) — производной функции f(x), определённой на интервале (−11; 3). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=-x−7 или совпадает с ней.

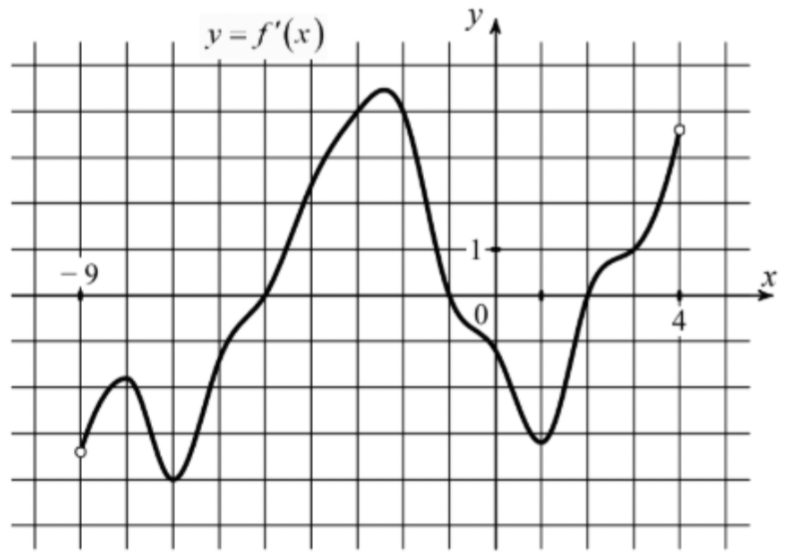
На рисунке изображён график функции y=f'(x) — производной функции f(x), определённой на интервале (−9; 4). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=2x−9 или совпадает с ней.

Найдите значение выражения 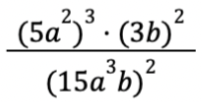при а = log₃5 и b = log₃15.

Найдите значение выражения 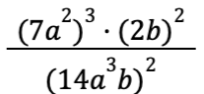при а = log₂7 и b = log₂14.

Найдите значение выражения 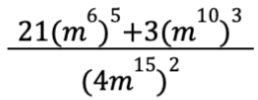при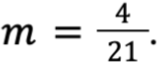

Найдите значение выражения 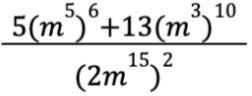при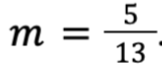

Решите уравнение 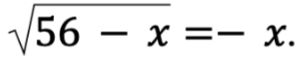Если уравнение имеет больше одного корня, в ответе запишите больший из корней.

Решите уравнение 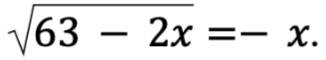Если уравнение имеет больше одного корня, в ответе запишите больший из корней.

Решите уравнение 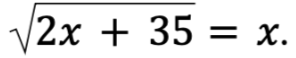. Если уравнение имеет больше одного корня, в ответе запишите меньший из корней.

Решите уравнение 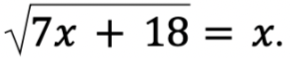Если уравнение имеет больше одного корня, в ответе запишите меньший из корней.