Банк заданий ЕГЭ по профильной математике - страница 178

Найдите объём многогранника, вершинами которого являются точки B, C, E, F, B₁, C₁, E₁, F₁ правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 12, а боковое ребро равно 15.

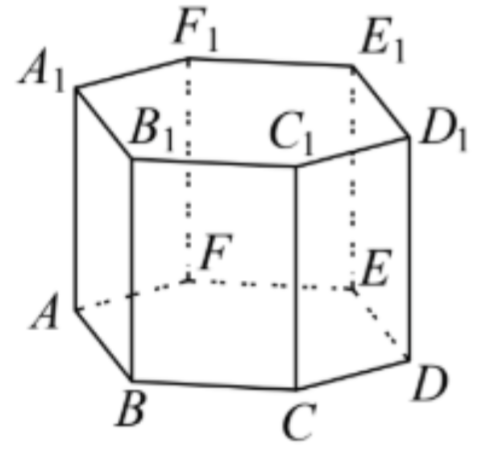
Найдите объём многогранника, вершинами которого являются точки B, C, E, F, B₁, C₁, E₁, F₁ правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 10, а боковое ребро равно 12.

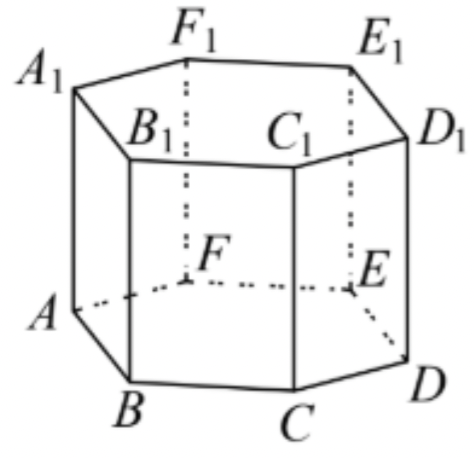
Длины векторов равны 3√5 и 4√10 , а угол между ними равен 45°. Найдите скалярное произведение

Длины векторов равны 6√6 и 5√3, а угол между ними равен 45°. Найдите скалярное произведение

Длины векторов равны 8 и 15 соответственно, а угол между ними равен 120°. Найдите скалярное произведение

Длины векторов равны 10 и 13 соответственно, а угол между ними равен 120°. Найдите скалярное произведение

Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 70°? Ответ дайте в градусах.

Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 30°? Ответ дайте в градусах.

Сумма двух углов параллелограмма равна 82°. Найдите один из оставшихся углов. Ответ дайте в градусах.

Сумма двух углов параллелограмма равна 46°. Найдите один из оставшихся углов. Ответ дайте в градусах.