Банк заданий ЕГЭ по профильной математике - страница 175

Теплоход проходит по течению реки до пункта назначения 560 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 8 часов, а в пункт отправления теплоход возвращается через 56 часов после отплытия из него. Ответ дайте в км/ч.

Теплоход проходит по течению реки до пункта назначения 320 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 2 км/ч, стоянка длится 4 часов, а в пункт отправления теплоход возвращается через 40 часов после отплытия из него. Ответ дайте в км/ч.

Теплоход проходит по течению реки до пункта назначения 780 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 28 км/ч, стоянка длится 4 часа, а в пункт отправления теплоход возвращается через 60 часов после отплытия из него. Ответ дайте в км/ч.

Теплоход проходит по течению реки до пункта назначения 280 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 17 км/ч, стоянка длится 6 часов, а в пункт отправления теплоход возвращается через 40 часов после отплытия из него. Ответ дайте в км/ч.

Некоторая компания продаёт свою продукцию по цене p = 500 рублей за единицу, переменные затраты на производство одной единицы продукции составляют v = 200 рублей, постоянные расходы предприятия составляют f = 500 000 рублей в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле π(q) = q(p - v) - f. Определите месячный объём производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет равна 700 000 рублей.

Некоторая компания продаёт свою продукцию по цене p = 700 рублей за единицу, переменные затраты на производство одной единицы продукции составляют v = 300 рублей, постоянные расходы предприятия составляют f = 700 000 рублей в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле π(q) = q(p - v) - f. Определите месячный объём производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет равна 500 000 рублей.

Зависимость объёма спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. рублей за единицу) задаётся формулой q = 85 - 5p. Выручка предприятия r (в тыс. рублей за месяц) вычисляется по формуле r(p) = q * p. Определите наибольшую цену p, при которой месячная выручка r(p) составит не менее 300 тыс. рублей. Ответ дайте в тысячах рублей за единицу.

Зависимость объёма спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. рублей за единицу) задаётся формулой q = 70 - 2p. Выручка предприятия r (в тыс. рублей за месяц) вычисляется по формуле r(p) = q * p. Определите наибольшую цену p, при которой месячная выручка r(p) составит не менее 600 тыс. рублей. Ответ дайте в тысячах рублей за единицу.

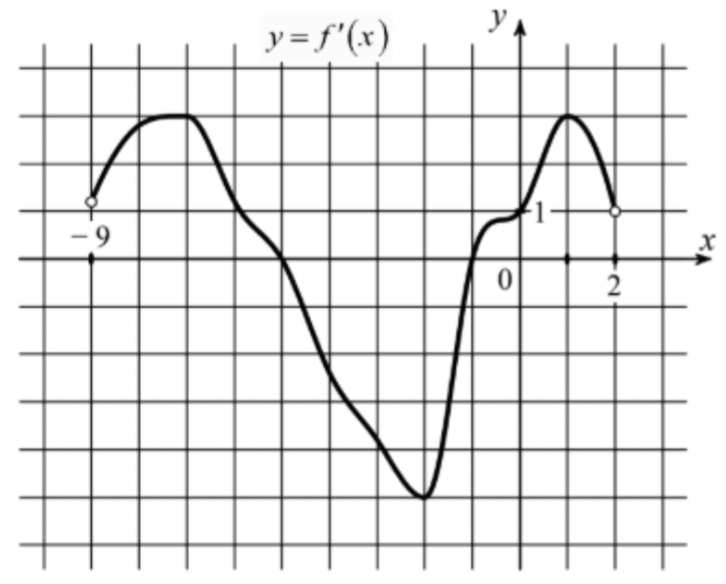
На рисунке изображён график функции y=f'(x) — производной функции f(x), определённой на интервале (−9; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=-x+16 или совпадает с ней.

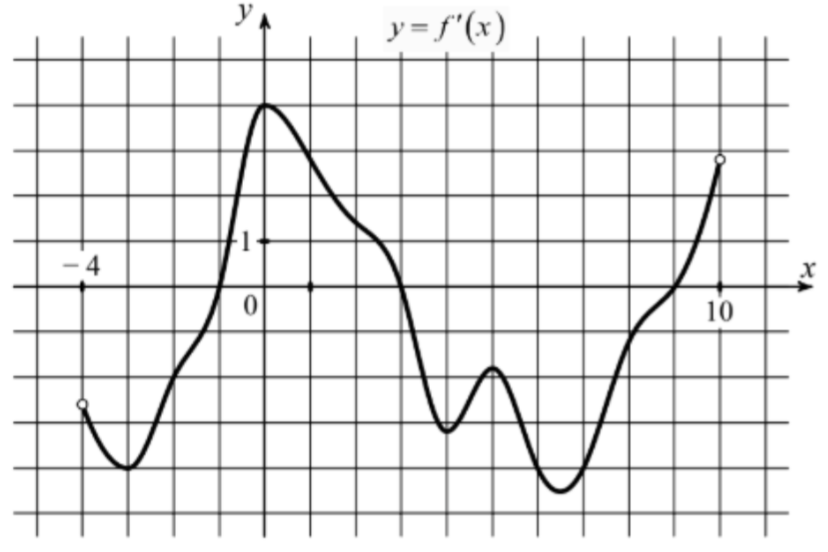
На рисунке изображён график функции y=f'(x) — производной функции f(x), определённой на интервале (−4; 10). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=-x−20 или совпадает с ней.