Найдите наименьшее значение функции у=x³-12x+5 на отрезке [0; 3]
Найдите наименьшее значение функции у=x³-27x+19 на отрезке [0; 4]
Найдите наибольшее значение функции y=23x-20sinx+24 на отрезке [-π/2; 0].
Найдите наибольшее значение функции y=55x-52sinx+40 на отрезке [-π/2; 0].
Найдите наименьшее значение функции y=7cosx-17x+7 на отрезке [-3π/2; 0].
Найдите наименьшее значение функции y=13cosx-17x+6 на отрезке [-3π/2; 0].
На рисунке изображён график функции f(x)=ax²+bx+c. Найдите значение f(-1).
На рисунке изображён график функции f(x)=ax²+bx+c. Найдите значение f(1).
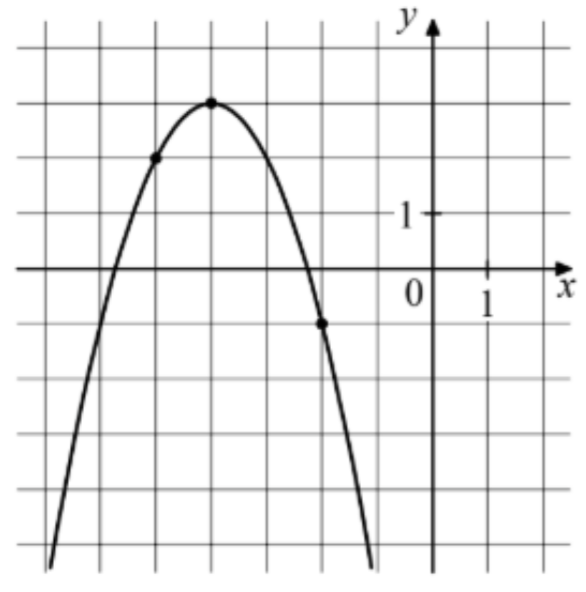
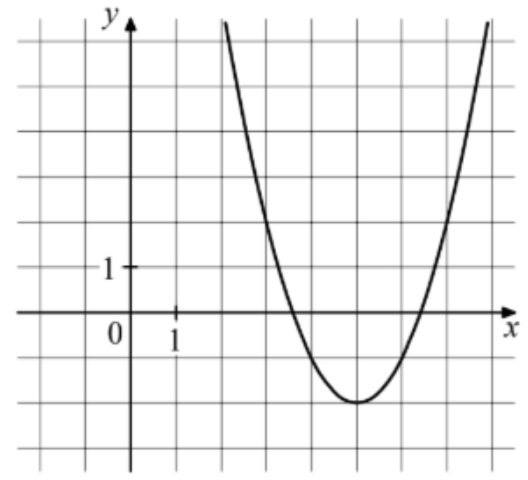
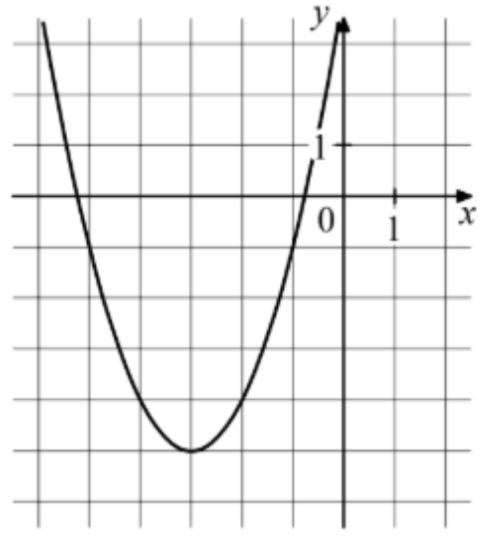
На рисунке изображён график функции f(x)=ax²+bx+c. Найдите значение f(-2).
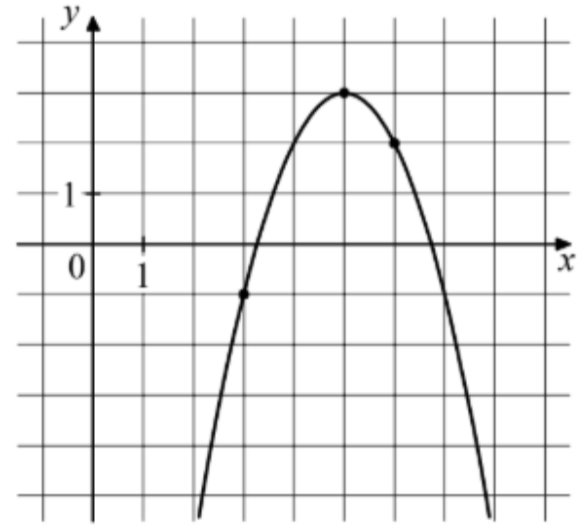
На рисунке изображён график функции f(x)=ax²+bx+c. Найдите значение f(2)
