Банк заданий ЕГЭ по профильной математике

Найдите значение выражения 6cos2α, если sinα = −0,8.

На рисунке изображён график y = f '(х) — производной функции f(x). На оси абсцисс отмечено девять точек: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉. Сколько из этих точек принадлежит промежуткам убывания функции f(x)?

Мотоциклист, движущийся по городу со скоростью v₀ = 60 км/ч , выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением a=32км/ч². Расстояние (в км) от мотоциклиста до города вычисляется по формуле 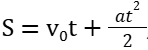, где t — время (в часах), прошедшее после выезда из города. Определите время, прошедшее после выезда мотоциклиста из города, если известно, что за это время он удалился от города на 154 км. Ответ дайте в минутах.

Один мастер может выполнить заказ за 42 часа, а другой — за 21 час. За сколько часов выполнят этот заказ оба мастера, работая вместе?

На рисунке изображены графики функций 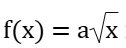и g(x)= kx, пересекающиеся в точках A и B. Найдите абсциссу точки B.

Найдите точку минимума функции y = (8х² - 40х + 40)*е^х+4.

Острый угол B прямоугольного треугольника ABC равен 21°. Найдите величину угла между биссектрисой CD и медианой CM, проведёнными из вершины прямого угла C. Ответ дайте в градусах. 

 В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известно, что BC=9, CD=3, CC₁=7. Найдите объём многогранника, вершинами которого являются точки A, B, C, D, C₁.

Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Изумруд» играет два матча с разными командами. Найдите вероятность того, что в этих матчах команда «Изумруд» начнёт игру с мячом не больше одного раза.

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в первом автомате закончится кофе, равна 0,1. Вероятность того, что кофе закончится во втором автомате, такая же. Вероятность того, что кофе закончится в двух автоматах, равна 0,05. Найдите вероятность того, что к концу дня кофе останется в двух автоматах.