Банк заданий ЕГЭ по профильной математике
Вопросы
В четырёхугольник ABCD вписана окружность, AB = 10, CD = 17. Найдите периметр четырёхугольника ABCD.
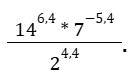
Через среднюю линию основания правильной треугольной призмы, объём которой равен 84, проведена плоскость, параллельная боковому ребру. Найдите объём отсечённой треугольной призмы.
На рисунке изображён график функции у=f(x), определённой на интервале (-5;4). Найдите корень уравнения f’(x) = 0.
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 299 МГц. Скорость погружения батискафа V (в м/с) вычисляется по формуле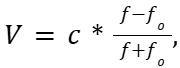 
где с = 1500 м/с - скорость звука в воде, fo - частота испускаемых импульсов (в МГц), f - частота отражённого от дна сигнала (в МГц), регистрируемая приёмником. Определите частоту отражённого сигнала, если скорость погружения батискафа равна 5 м/с. Ответ дайте в МГц.
Имеется два сосуда. Первый содержит 40 кг, а второй - 25 кг растворов кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 30 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 36 % кислоты. Сколько процентов кислоты содержится в первом сосуде?
На рисунке изображены графики функций видов f(x)=kx и g(x)=ax+b, пересекающиеся в точках А и В. Найдите абсциссу точки В.
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля качества. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
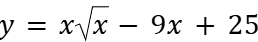на отрезке [1; 50].Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 12, но не дойдя до отметки 3.