Банк заданий ЕГЭ по информатике - страница 119
Вопросы
Квадрат разлинован на N × N клеток (1 < N < 26). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку; по команде вниз –– в соседнюю нижнюю. Робот разрушается при попытке выхода за границу квадрата или при попытке пересечения стены клетки. В таблице стены отмечены границами с утолщением.
Перед запуском Робота в каждой клетке квадрата указан бонус, который Робот забирает после посещения клетки. Размер бонуса в каждой клетке –– это натуральное число, не превышающее 100. Это правило относится к начальной и конечной клеткам маршрута Робота.
Определите минимальную и максимальную суммы бонусов, которые может собрать Робот, перемещаясь из левой верхней клетки квадрата в его правую нижнюю клетку. В ответе укажите два числа: сначала минимальную сумму, затем максимальную.
Исходные данные представлены в форме электронной таблицы размером
N × N, в которой одна ячейка соответствует одной клетке квадрата. Стены, через которые Роботу нельзя проходить, отмечены в электронной таблице границами с утолщением.
В ответ укажите два числа через пробел – сначала минимальную сумму, затем максимальную
Все шестибуквенные слова, составленные из букв П, Я, Т, Н, И, Ц, А, записаны в алфавитном порядке и пронумерованы.
Вот начало списка:
1. АААААА
2. АААААИ
3. АААААН
4. АААААП
5. АААААТ
6. АААААЦ
7. АААААЯ
…
Определите в этом списке количество слов с чётными номерами, которые не начинаются с буквы Н и при этом содержат в своей записи ровно две буквы Я.
Миша заполнял таблицу истинности логической функции F
((w → y) → (x ≡ y)) \/ ¬z,
но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
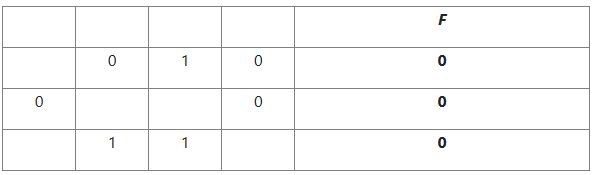
Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. Далее эта запись обрабатывается по следующему правилу:
а) если число N делится на 3, то к этой записи дописываются три последние двоичные цифры;
б) если число N на 3 не делится, то остаток от деления умножается на 3, переводится в двоичную запись
и дописывается в конец числа.
Полученная таким образом запись является двоичной записью искомого числа R.
3. Результат переводится в десятичную систему и выводится на экран.
Например, для исходного числа 12 = 11002 результатом является число 11001002 = 100, а для исходного числа 4 = 1002 это число 100112 = 19.
Укажите максимальное число R, не превышающее 138, которое может быть получено с помощью описанного алгоритма. В ответе запишите это число в десятичной системе счисления.
Определите количество шестизначных чисел, записанных в шестеричной системе счисления, в записи которых ровно одна цифра 2, при этом никакая нечётная цифра не стоит рядом с цифрой 2.
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу: если N нечётное, в конец числа (справа) дописывается сначала ноль, а затем единица. В противном случае, если N чётное, справа дописывается сначала единица, а затем ноль.
Например, двоичная запись 1001 числа 9 будет преобразована в 100101, а двоичная запись 1100 числа 12 будет преобразована в 110010.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа R – результата работы данного алгоритма.
Укажите минимальное число R, которое больше 74 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 1; для буквы Б – кодовое слово 01. Какова наименьшая возможная сумма длин кодовых слов для букв В, Г, Д, Е?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
На рисунке схема дорог N-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).
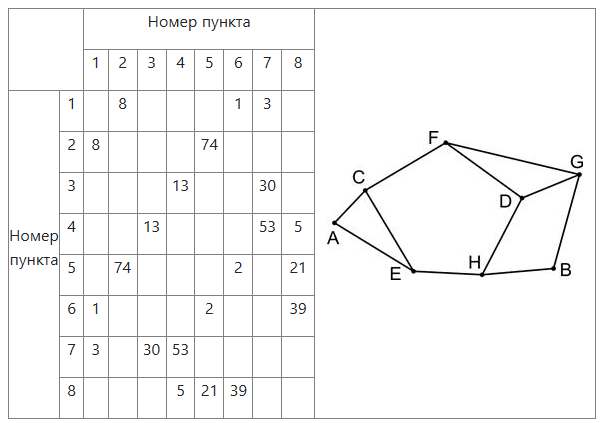
Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта A в пункт C и из пункта B в пункт H.
В ответе запишите целое число.
Прибор автоматической фиксации нарушений правил дорожного движения делает цветные фотографии размером 1024×768 пикселей, используя палитру из 4096 цветов. Снимки сохраняются в памяти камеры, группируются в пакеты по несколько штук, а затем передаются в центр обработки информации со скоростью передачи данных 1 310 720 бит/с. Каково максимально возможное количество снимков в одном пакете, если на передачу одного пакета отводится не более 300 секунд?
В ответе запишите целое число.
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).
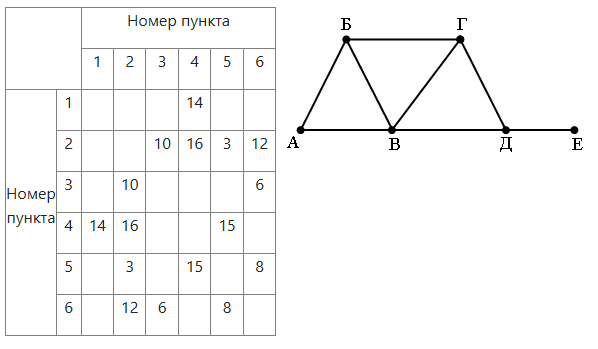
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова протяжённость дороги из пункта В в пункт Г. В ответе запишите целое число – так, как оно указано в таблице.
